Descripción

Este es un ejemplo donde se compara la metodología tradicional de agendamiento mediante pits anidados y el agendamiento directo de bloques sobre un modelo de bloques específico. 

Agendamiento mediante pits anidados

El agendamiento mediante pits anidados corresponde a utilizar el algoritmo de Lerchs y Grossmann (u otro) sobre una serie de valorizaciones del modelo de bloques, parametrizadas por un multiplicador del precio o "revenue factor". A partir de los pits anidados generados de esta forma, se seleccionan pushbacks o "candidatos a fase", que sirven de guía para el diseño, y a continuación, son agendados para extracción en el tiempo.

Agendamiento directo de bloques

El agendamiento directo de bloques es un enfoque alternativo que pone énfasis en la temporalidad del problema y el costo de oportunidad, buscando resolver desde un principio el problema de en qué momento del tiempo es más conveniente extraer un bloque y cuál es la mejor decisión de procesamiento (incluyendo la opción de lastre). Tradicionalmente esta metodología se apoya en modelos de programación lineal de gran tamaño.

Resumen

En este experimento se compara el agendamiento de la producción de una mina a rajo abierto mediante dos metodologías: (i) utilizando pits anidados y a partir de ahí generando dos estrategias de extracción, una pit por pit de manera incremental, conocida en la literatura como "Best Case" y otra estrategia que extrae banco a banco, conocida como "Worst Case". Luego, (ii) mediante agendamiento directo de bloques, donde se plantea el problema utilizando modelos de programación lineal y se utilizan diversas estrategias para resolverlo, en particular, en este ejemplo mostraremos dos: utilizando una heuristica por ventanas, la cual llamaremos STW, y otra, utilizando una heuristica Toposort, la que llameremos TOPO. En ambas estrategias, se imponen restricciones sobre los tonelajes extraídos. No se hacen consideraciones de diseño.

En los cuatro casos, se analizan sus geometrías de extraccción, tonelajes de mineral y lastre, y valor descontado acumulado a lo largo de la vida del proyecto. En términos de valor, las estrategias de agendamiento directo de bloques muestran el mejor desempeño.

	Estrategia	Valor acumulado descontado [MUSD]
PITS ANIDADOS	WORST CASE   BEST CASE	1.306 1.372
DIRECTO BLOQUES	STW   TOPO	1.386   1.390

 

A continuación, se muestra el desarrollo del experimento, con todos los detalles de su implementación en DOPPLER.

 

Modelo de Bloques

Nombre	MDB RAJO
Número de Bloques	151.898
Dimensiones	5 x 5 x 5
Rangos de Coordenadas	X=214.961,125 - 215.251,125 Y=8.080.666,5 - 8.081.201,5 Z=247,5 - 422,5
Columnas en el Modelo (aparte de coordenadas)	zone cu au ag density
Comentarios	Se agregó columna de tonelaje

VISUALIZACION DEL MODELO

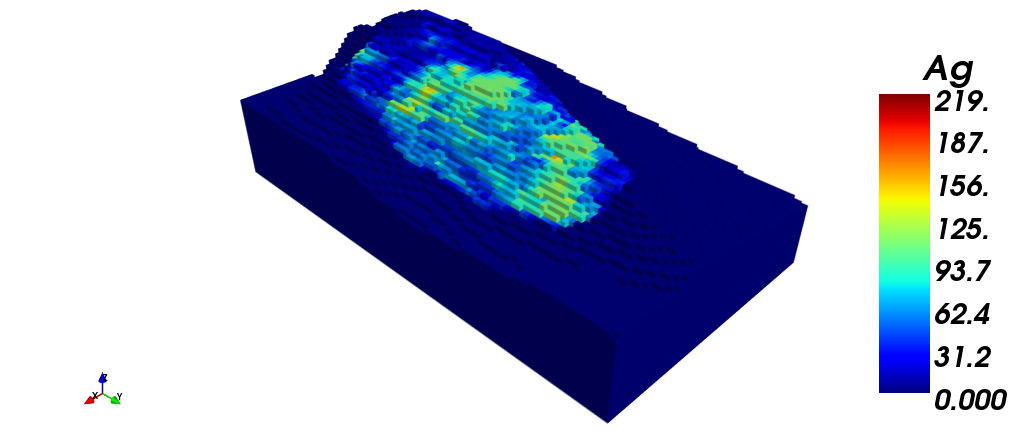
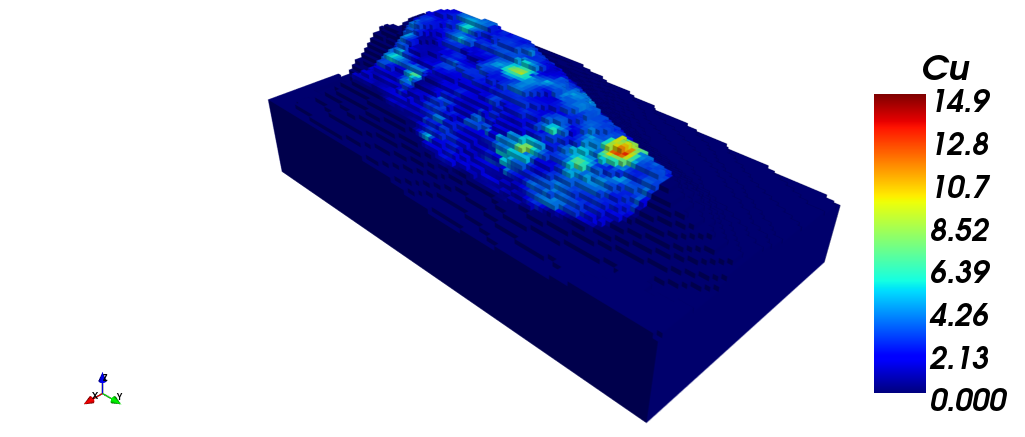
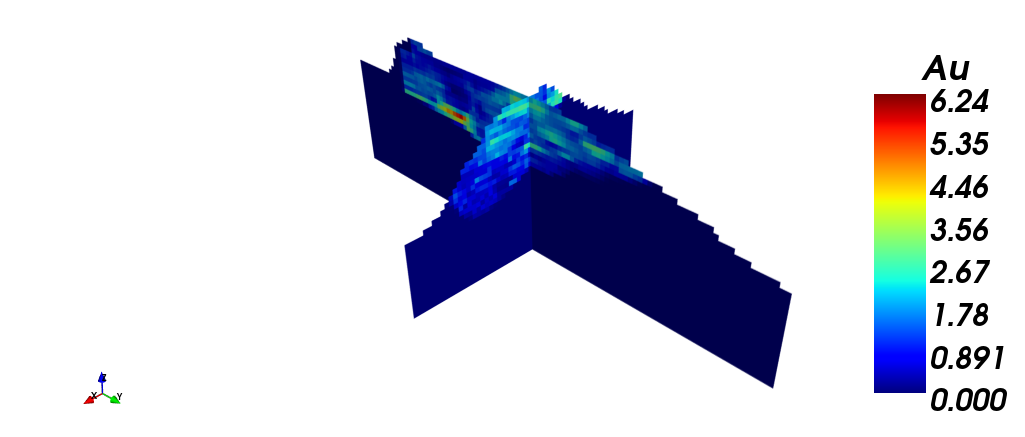
En las siguientes imagenes, se muestran el modelo de bloques con: (i) ley de plata (ag) en cada bloque, (ii) ley de cobre (cu) y (iii) ley de oro (au). Finalmente se muestra (iv) una vista en dos secciones, filtrado por ley de oro.

(i)	(ii)
(iii)	(iv)

 

CURVAS TONELAJE LEY

 A continuación, se presentan tres curvas tonelaje ley, una para cada tipo de metal: (i) plata (ag), (ii) oro (au) y (iii) cobre (cu) contenidos en el modelo de bloques.

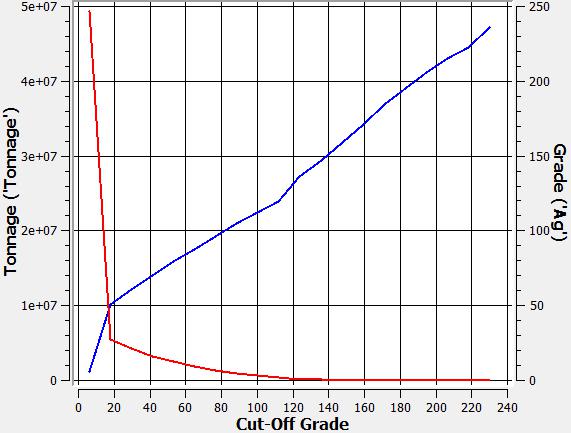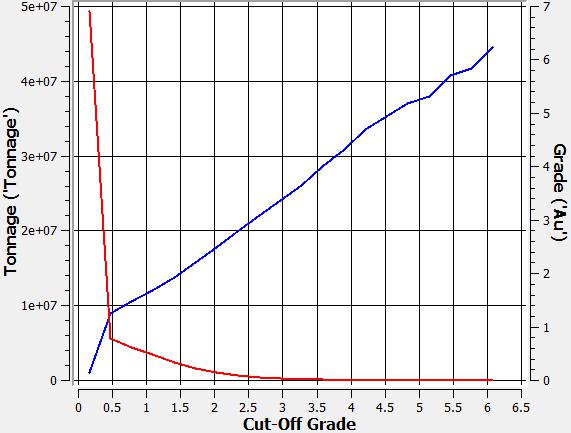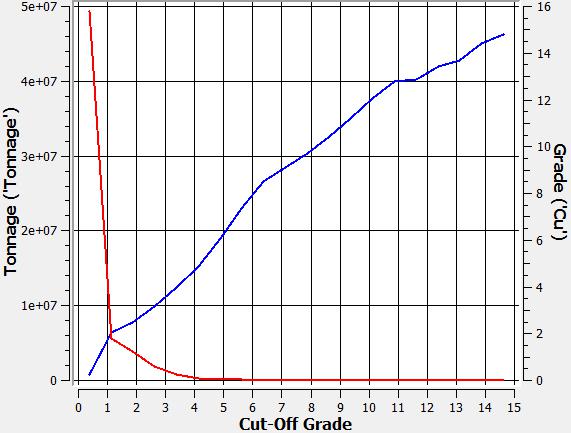(i)	(ii)	(iii)

 

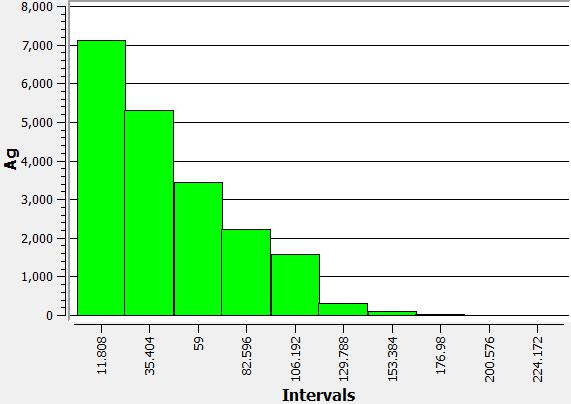
DISTRIBUCION DE LEYES

Para cada tipo de metal en el modelo de bloques: (i) plata (ag), (ii) oro (au) y (iii) cobre (cu), se muestran las distribuciones de ley.

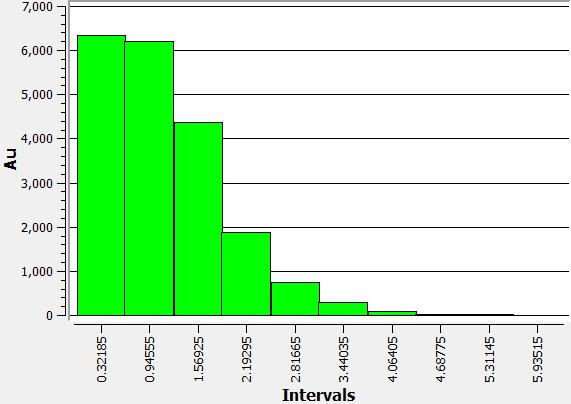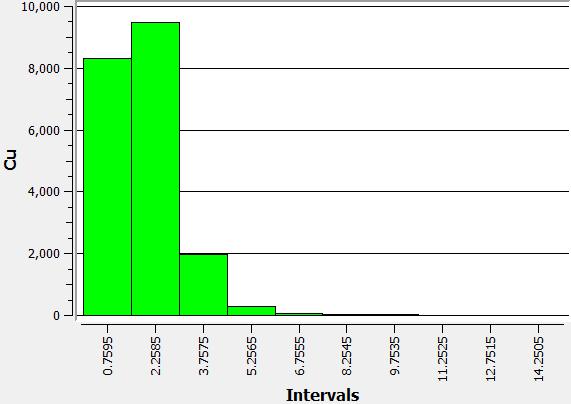(i)	(ii)	(iii)

 

Pit Final

Valorización y Ángulo de Talud

Datos para valorización:

1) Precio del metal: Ag = 16 [USD/oz]; Au = 1.100 [USD/oz]; Cu = 2,0 [USD/lb] 

2) Costo de venta: Ag = 1,6 [USD/oz]; Au = 100 [USD/oz]; Cu = 0,3 [USD/lb] 

3) Costo de proceso: Ag = 8,0 [USD/Ton]; Au = 8,2 [USD/Ton]; Cu = 8,0 [USD/Ton]

4) Recuperación metalúrgica: Ag = 0,77; Au = 0,76; Cu = 0,85

5) Costo de Mina: 1,5 [USD/Ton]

Datos para ángulo de talud:

1) 48° (global)

Visualización de pit final

A continuación, se muestra el pit final obtenido a partir de los modelos de bloque y económico proporcionados, (i) vista isométrica y (ii) vista en sección.

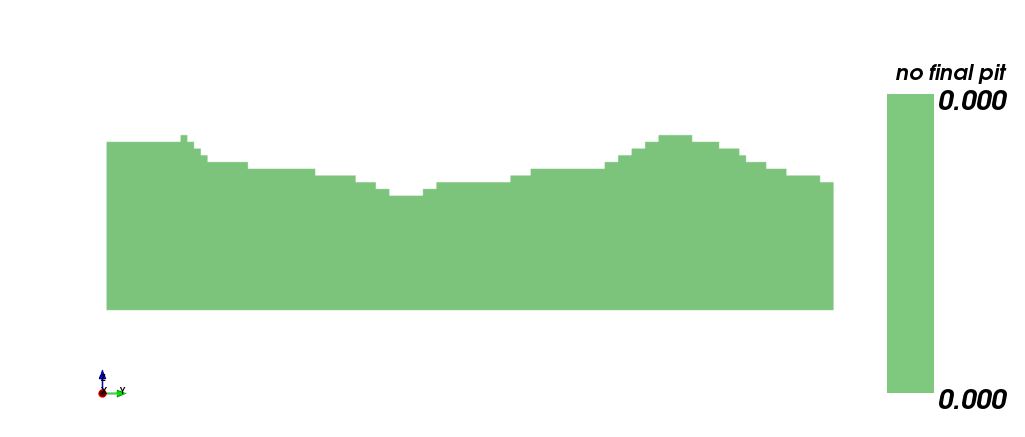(i)	(ii)

 

Pits Anidados

Valorización y Ángulo de Talud

Se utilizaron los mismos datos para valorización del caso anterior de pit final, pero utilizando una serie de ponderadores sobre el precio (revenue factors), donde para cada uno de ellos, se obtiene un pit anidado. 

La familia de revenue factors (RF) seleccionada va desde 0,00 hasta 1,00, utilizando un paso de 0,05 entre factores sucesivos. 

 

Gráfico Pit By Pit

 

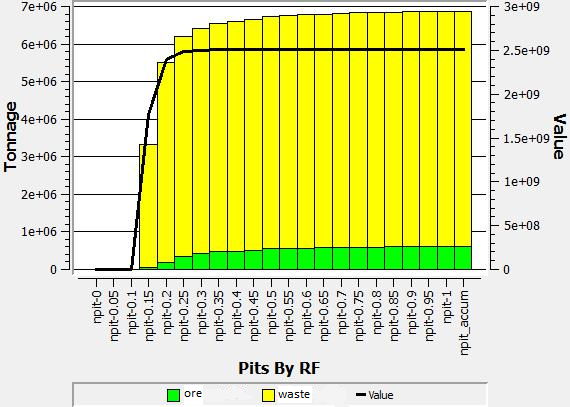
Visualización de pits anidados

En las siguientes figuras, se muestra la familia de pits anidados obtenida a partir de la elección de los revenue factors: (i) muestra una vista isométrica de los pits anidados dentro de la envolvente económica, mientras que (ii) muestra una vista en sección. Cabe destacar que el primer pit que "flota" es aquel que corresponde a un RF= 0,15.

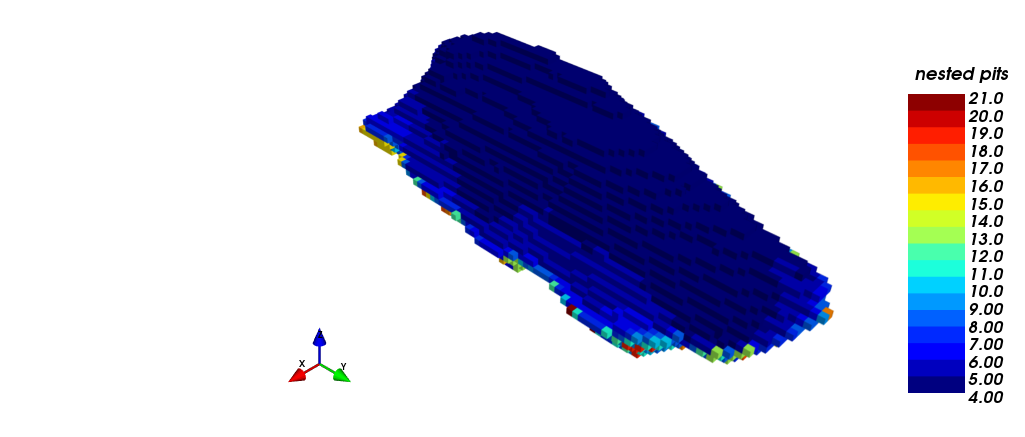(i)	(ii)

 

Best & Worst Cases

PLAN DE PRODUCCIÓN BEST CASE

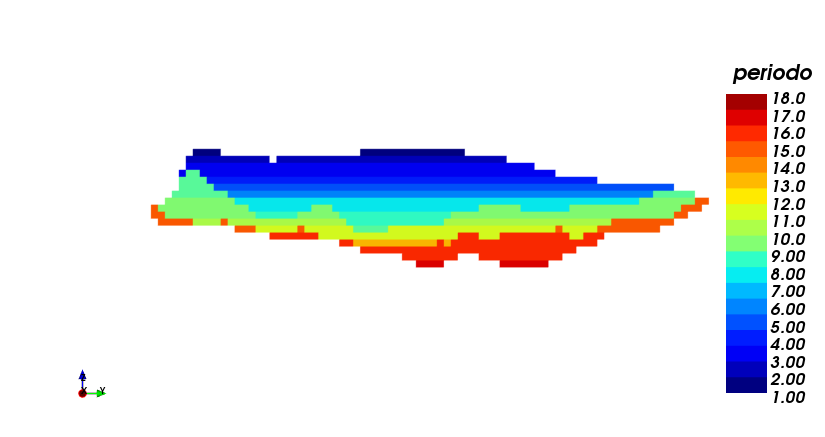
Este caso corresponde cuando la extraccción se realiza siguiendo el orden de los pits anidados (pit por pit). Se impuso un límite en el tonelaje extraído de 400.000 [Ton], con el cual se obtuvo un horizonte de 18 periodos (anuales). No se dispone de la opción de restringir el mineral a planta en este módulo. Note que la producción alcanzó el máximo en varios periodos, dejando para el final del horizonte las mayores porciones de lastre: (i) muestra el plan de producción, y (ii) muestra una vista en sección del agendamiento, ambos utilizando una estrategia "best case", pit por pit.

NPV Best Case: 1.372 [MUSD]

(i)	(ii)

 

PLAN DE PRODUCCIÓN WORST CASE

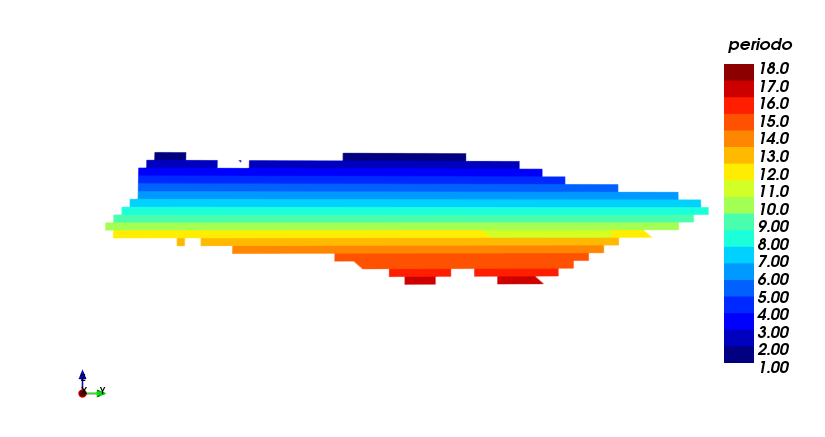
Este caso corresponde cuando la extraccción se realiza siguiendo el orden banco a banco. Igual que antes, se impuso un límite en el tonelaje extraído de 400.000 [Ton] y se obtuvieron 18 periodos. No se dispone de la opción de restringir el mineral a planta en este módulo. Nótese que tanto la producción como el lastre en este caso se distribuyen de manera más uniforme a lo largo del horizonte del proyecto. Sin embargo, no se aprecian diferencias más allá de las mencionadas entre este caso y el anterior: (i) muestra el plan de producción, y (ii) muestra una vista en sección del agendamiento, ambos utilizando una estrategia "worst case", banco a banco.

NPV Worst Case: 1.306 [MUSD] 

(i)	(ii)

 

Agendamiento Directo de Bloques

En esta parte, se usarán modelos de agendamiento directo de bloques. Para su resolución, mostraremos dos estrategias utilizadas: (i) heurística por ventanas (STW), la cual resuelve de manera incremental el problema, utilizando una ventana de periodos (menor al horizonte) y fijando parte, o completamente, esa ventana como solución, y (ii) heurística Toposort (TOPO), la cual explota la relajación continua del problema y define los tiempos esperados para realizar un agendamiento utilizando el orden dado por los tiempos esperados y las capacidades de producción.

Parámetros de Entrada

Número de periodos: 18

Tasa de descuento: 10%

Ángulo de talud: 48° (global)

Valorizaciones por destino:

• Valor a planta: cada bloque se valoriza como si su destino final es planta.
• Valor a botadero: cada bloque se valoriza como si su destino final es botadero.

Capacidades por período:

• Mina: 400.000 [Ton]
• Planta: 350.000 [Ton]

 

Agendamiento eligiendo el proceso óptimo 

RESULTADOS HEURISTICA POR VENTANAS (STW) (ventana:1, paso: 1)

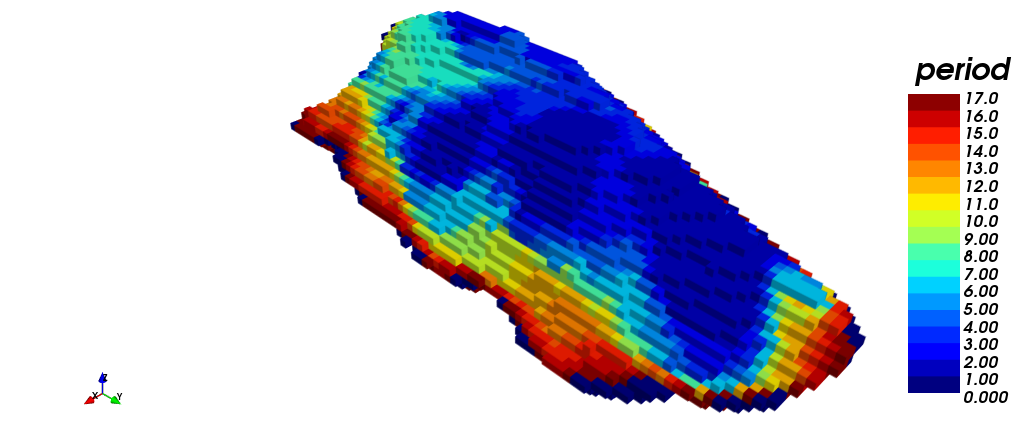
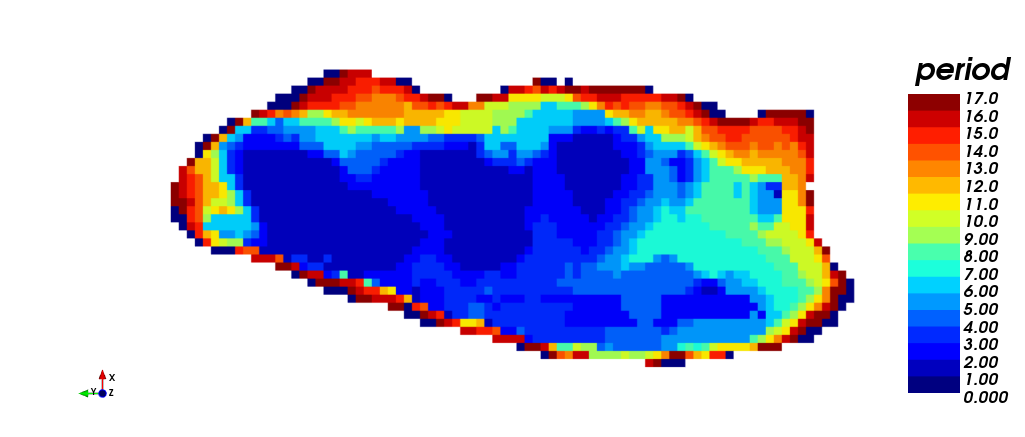
En las figuras a continuación se muestran distintas vistas del agendamiento en el tiempo obtenido mediante STW: (i) vista isométrica, (iii) vista en planta y (v) vista en sección. Note que esta estrategia requirió 17 periodos para agendar la producción. Por otra parte, se muestra el agendamiento por destino: (ii) vista isométrica, (iv) vista en planta, y (vi) vista en sección. En amarillo (1) se muestra lo que es enviado a planta, en rojo (2) lo que es enviado a botadero, y en azul (0) lo que nunca es extraído.

(i)	(ii)
(iii)	(iv)
(v)	(vi)

 

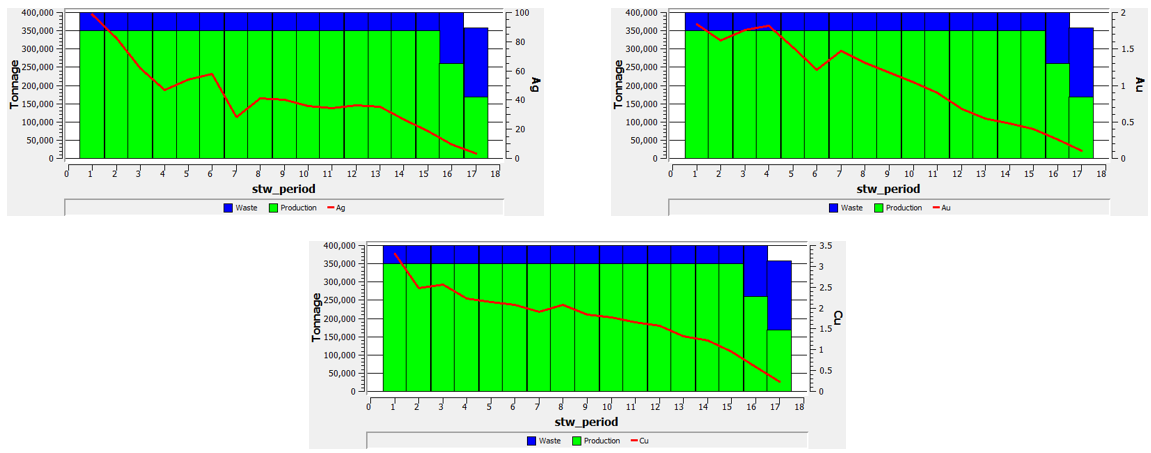
PLAN DE PRODUCCIÓN USANDO HEURISTICA POR VENTANAS (STW)

Se muestran los planes de producción (tonelajes de mineral y lastre), además de las leyes medias de cada metal por periodo.

 

RESULTADOS HEURISTICA TOPOSORT (TOPO)

En las figuras a continuación se muestran distintas vistas del agendamiento en el tiempo obtenido mediante TOPO: (i) vista isométrica, (iii) vista en planta y (v) vista en sección. Note que esta estrategia requirió los 18 periodos para agendar la producción, a diferencia de STW, que lo hizo en un periodo menos. Por otra parte, se muestra el agendamiento por destino: (ii) vista isométrica, (iv) vista en planta, y (vi) vista en sección. En amarillo (1) se muestra lo que es enviado a planta, en rojo (2) lo que es enviado a botadero, y en azul (0) lo que nunca es extraído. Note las diferencias de asignación entre ambas estrategias, STW y TOPO: muchos de los bloques que STW envía a botadero, TOPO los clasifica como mineral a planta.

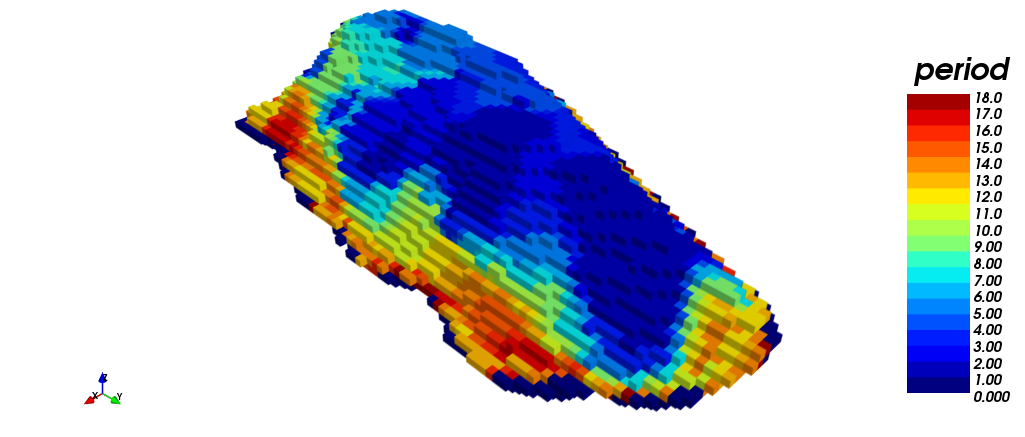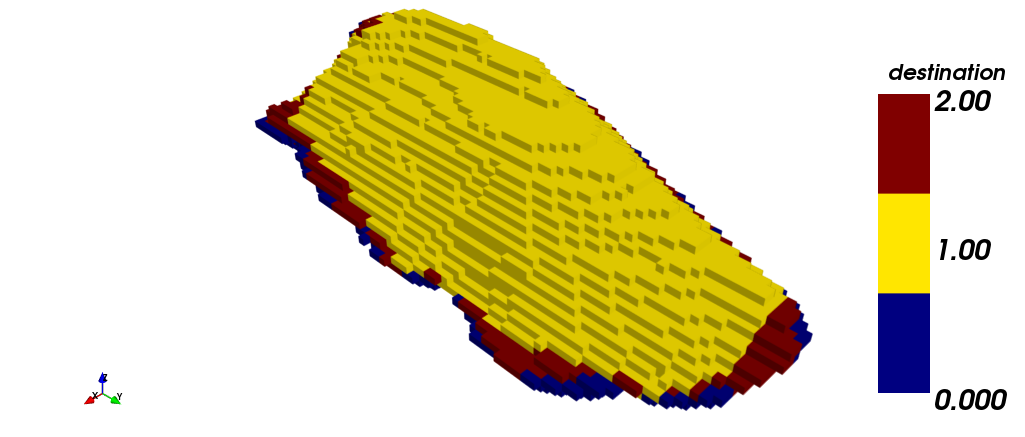(i)	(ii)
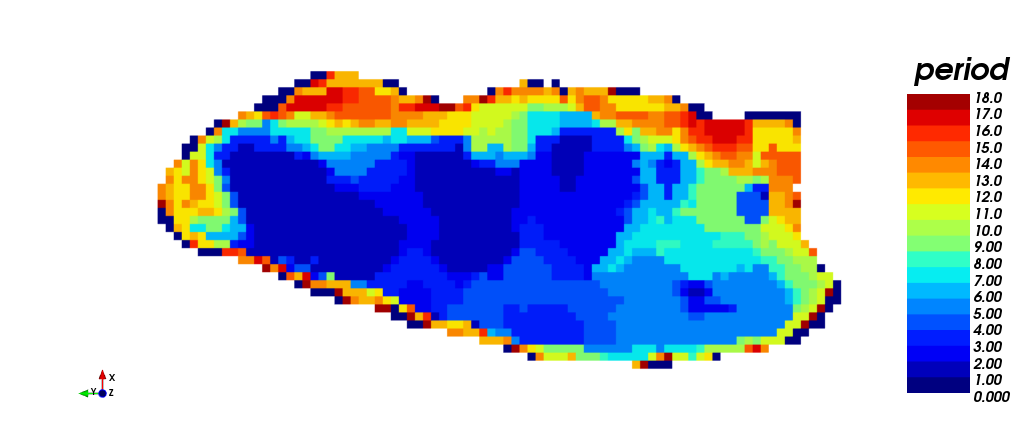(iii)	(iv)
(v)	(vi)

 

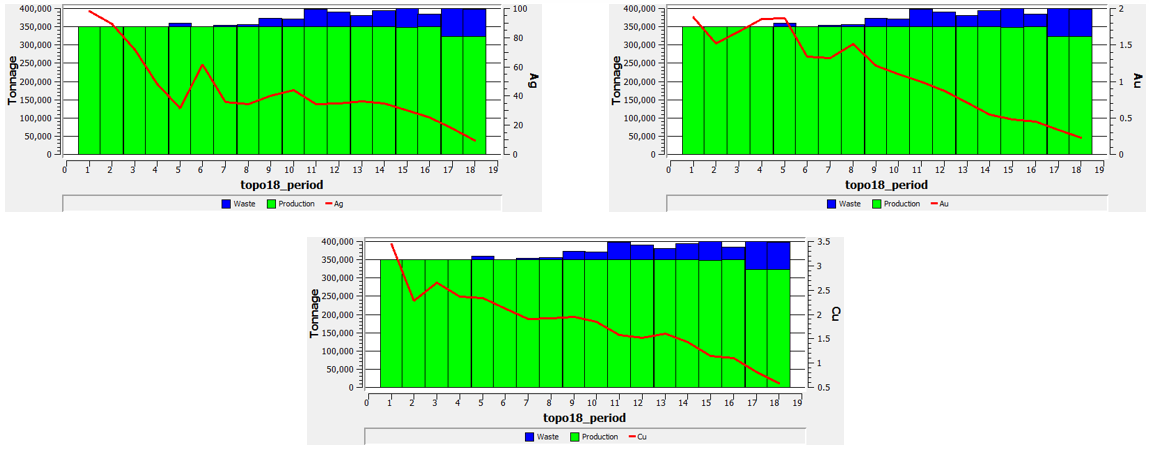
PLAN DE PRODUCCIÓN USANDO HEURISTICA TOPOSORT (TOPO)

Se muestran los planes de producción (tonelajes de mineral y lastre), además de las leyes medias de cada metal por periodo.

 

Comparación y conclusión

Considerando los resultados obtenidos por ambas heurísticas, se ve claramente que la heurística toposort agendó la producción en 18 periodos, tal como se pidió, mientras que la heurística por ventanas acortó la vida de la mina a 17 años. Mirando los planes de producción, TOPO pudo retrasar la entrada de lastre en los primeros periodos, clasificando como mineral todo el material extraído entre los periodos 1 y 4, además del 6, y desde ahí extrayendo de manera gradual el lastre hasta completar la capacidad de mina en los periodos finales. Por su parte, STW hace una extracción homogenea, saturando tanto las capacidades de mina y planta en la mayoría de los periodos (salvo 16 y 17). Por una parte, la característica "míope" de STW no le permite tomar decisiones mirando lo que podría hacer en periodos posteriores, tomando en cada periodo la mejor decisión posible. Por otra parte, TOPO es capaz de tomar una decisión "global" a partir de la información obtenida de la solución continua del problema original, por lo que en cierto sentido toma una decisión más robusta, pues para decidir sobre un periodo particular, lo hace mirando qué pasará en periodos posteriores.  

En términos de valor descontado acumulado (VAN), la estrategia TOPO muestra un VAN ínfimamente mayor al VAN de STW, de hecho, un 0,23% mayor. 

VAN STW  : 1.386 [MUSD]

VAN TOPO: 1.390 [MUSD]

En general, este tipo de estrategias no pueden asegurar encontrar una solución óptima al problema de agendamiento, sin embargo, son una buena alternativa considerando que en problemas reales de gran tamaño (en cuanto a número de bloques, periodos y destinos) se hace impracticable obtener la solución óptima por tratamiento directo del problema.