A continuación aplicaremos los conceptos anteriores de sumatorias y matrices para el cálculo de un pit con el máximo valor posible. Este es un problema muy importante de la planificación minera a cielo abierto, conocido como el problema del "pit final" ya que representa la envolvente del material a ser extraído mediante una operación a cielo abierto y que asegura la mayor utilidad para la compañía.
Para poder comprender este problema, primero debemos entender el concepto de ángulo de talud.
A continuación presentamos varias fotografías de distintas operaciones a cielo abierto del mundo. ¿Qué tienen en común?



Las operaciones a cielo abierto, o rajos, tienen una característica fundamental y es que las murallas de la excavación deben mantener cierto ángulo que asegure la estabilidad de estas murallas, a fin de mantener una operación segura. La siguiente imagen, real, ilustra el peligro al que estamos expuestos si se pierde esa estabilidad.

El ángulo de talud depende de cada operación minera y puede ser distinto según la zona dentro de una operación. Cuando la roca es más competente, el ángulo puede ser más empinado ya que es capaz de mantenerse estable en esas condiciones. En cambio, cuando la roca es menos competente (piensa por ejemplo el caso extremo de arena), el ángulo debe ser mucho más suave para asegurar que no existan deslizamientos.
Precedencias
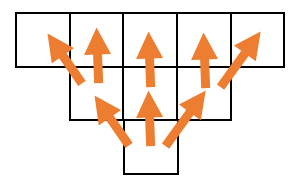
Si bien el ángulo de talud es un concepto geométrico, cuando trabajamos con los bloques de un modelo el ángulo puede representarse con precedencias que indican qué bloques deben ser extraídos con anterioridad a fin de asegurar el ángulo.
En nuestro ejemplo simple, podemos considerar que los ángulos son de 45 grados, con lo cual, en los bloques, las precedencias lucen de la forma siguiente
Ejemplo de pit final
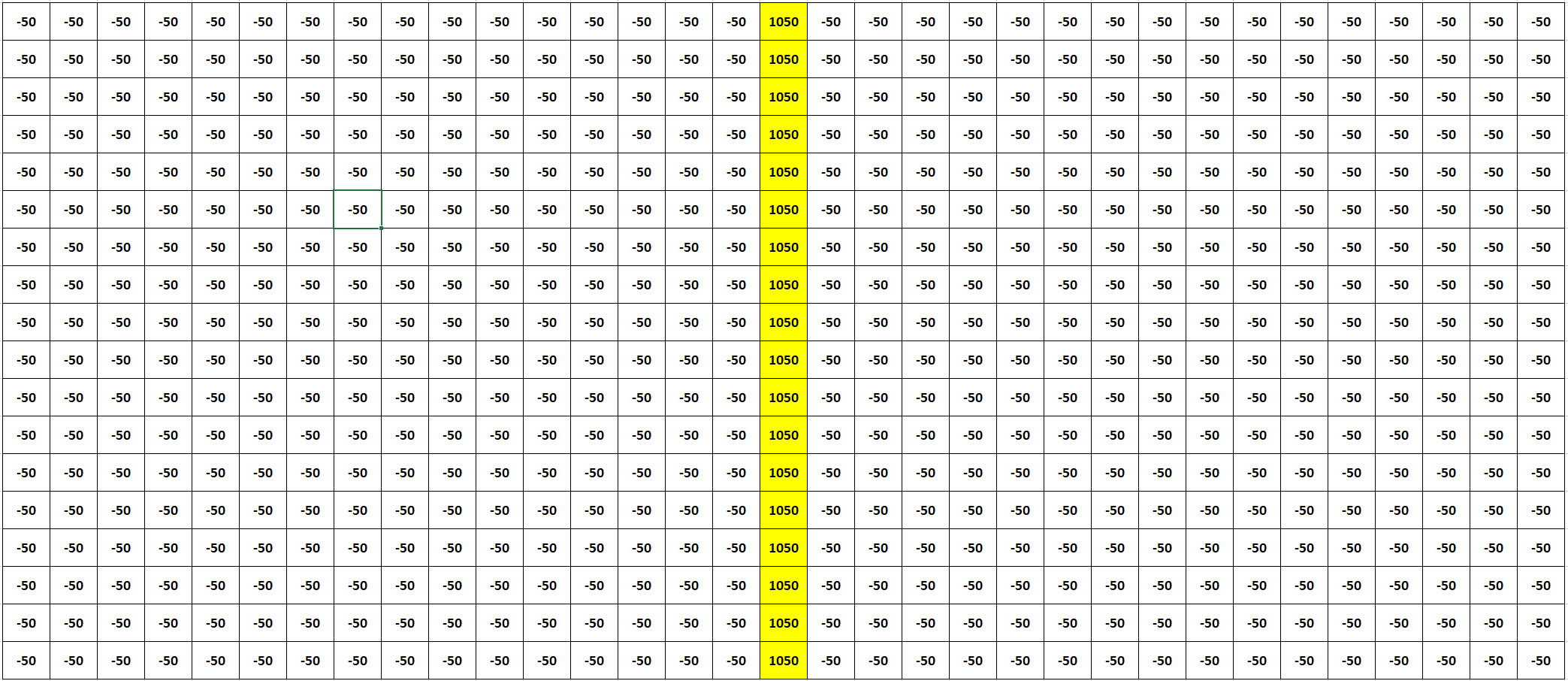
Volvamos ahora a nuestro ejemplo en 2-D, consideremos que el valor de los bloques está dado por la siguiente matriz. Este es un ejemplo ideal, ya que los depósitos de minerales ciertamente no tienen esta estructura tan particular.
Nos gustaría determinar el pit final en este caso, es decir, los bloques que debemos extraer de manera de maximizar el valor total, pero respetando un ángulo de 45 grados.
Preliminares
La siguiente imagen muestra tres posibles pits.
- El primer pit consiste de un solo bloque. Efectivamente, si solo pudieramos extraer un bloque, entonces eligiríamos en la superficie uno con beneficio 1050. El valor total de este pit es 1050.
- El segundo pit tiene dos niveles de profundidad. En este caso elegimos extraer 2 bloques de 105, pero eso nos obliga a extraer dos bloques de lastre, los cuales tienen un beneficio negativo de -50. El valor total de este pit es 1050+1050-50-50 = 2000.
- El tercer pit corresponde a la mejor solución posible con tres niveles. Extraemos tres bloques de mineral, pero esto nos fuerza a extraer 6 bloques de lastre. El valor total de este pit es 1050+1050+1050-50-50-50-50-50-50=2850.
Cada vez que decidimos extraer un nivel más ganamos 1050 adicionales, pero... ¿qué pasa con el lastre?
Solución algebraica
Para poder determinar cuál es la profundidad óptima tenemos que determinar el valor de k que nos permite alcanzar el máximo beneficio. Hasta ahora sabemos que no es k=1 ni k=2, ya que al menos con k=3 ganamos más. ¿Cuál será la profundidad ideal?
Necesitamos determinar el valor económico total. Este corresponde a la suma de los bloques que aportan valor, menos el valor del lastre que extraigamos, es decir
$$\Large{V=I-C}$$
Ingreso total como función de la profundidad
Calcular el ingreso (valores positivos) no es difícil. Ya observamos que si el pit tiene k niveles, hay exactamente k bloques amarillos. Es decir, el ingreso total lo podemos calcular como
$$\Large{I(k)=1050k}$$
Así, por ejemplo, si el pit tiene 10 niveles, entonces el ingreso total es I(10) = 10500. Observar que escribimos I(k), ya que podemos entender el ingreso como una función de la profundidad, es decir, para cada valor de k, tenemos un valor del ingreso y que está dado por la expresión anterior.
Costo total en función de la profundidad
El ejemplo que estamos ejecutando tiene una ventaja y es que todos los bloques de lastre tienen el mismo costo: -50, así que para saber el costo total necesitamos "basta con saber" el número de bloques de lastre. Veamos:
- Cuado k=1, no hay ningún bloque de lastre, así que C(1)=0.
- Cuando k=2, hay dos bloques, así que C(2)=2*50 = 100.
- Cuando k=3, hay 6 bloques, es decir C(3)=6*50=300.
- Cuando k=4 hay 12 bloques: C(4)=12*50=600.
Para poder determinar el número de bloques a la profundidad k, podemos inspirarnos en el pequeño Gauss. Observamos lo siguiente: Si miramos cuántos bloques de lastre hay al lado izquierdo de la columna de mineral cuando el pit tiene k niveles tenemos que:
- En el nivel k no hay ningún bloque de lastre
- En el nivel k-1 hay exactamente 1 bloque de lastre (lado izquierdo solamente)
- En el nivel k-2 hay 2 bloques de lastre
- En el nivel k-3 hay 3 bloques...
- Finalmente en el nivel 1 hay k-1 bloques.
Es decir, el número de bloques de lastre al lado izquierdo es
$$\Large{1+2+3+ \dots + (k-1) = \sum_{i=1}^{k-1} i }$$
O sea precisamente la suma de los primeros k-1 números naturales. Afortunadamente, ya sabemos cuánto es su valor...
$$\Large{\sum_{i=1}^{k-1}i=\frac{(k-1)k}{2}}$$
Es decir, si consideramos ahora el total de bloques, tato a la derecha como izquierda, tenemos en total (k-1)k bloques, donde cada uno nos cuesta 50. De esta forma el costo total al nivel k es
$$\Large{C(k)=50k(k-1)}$$
Valor del pit en función de la profundidad
Finalmente, podemos escribir una fórmula para el valor total como
$$\Large{V(k)=1050k - 50k(k-1) = -50k^2 + 1100k}$$
Solución gráfica
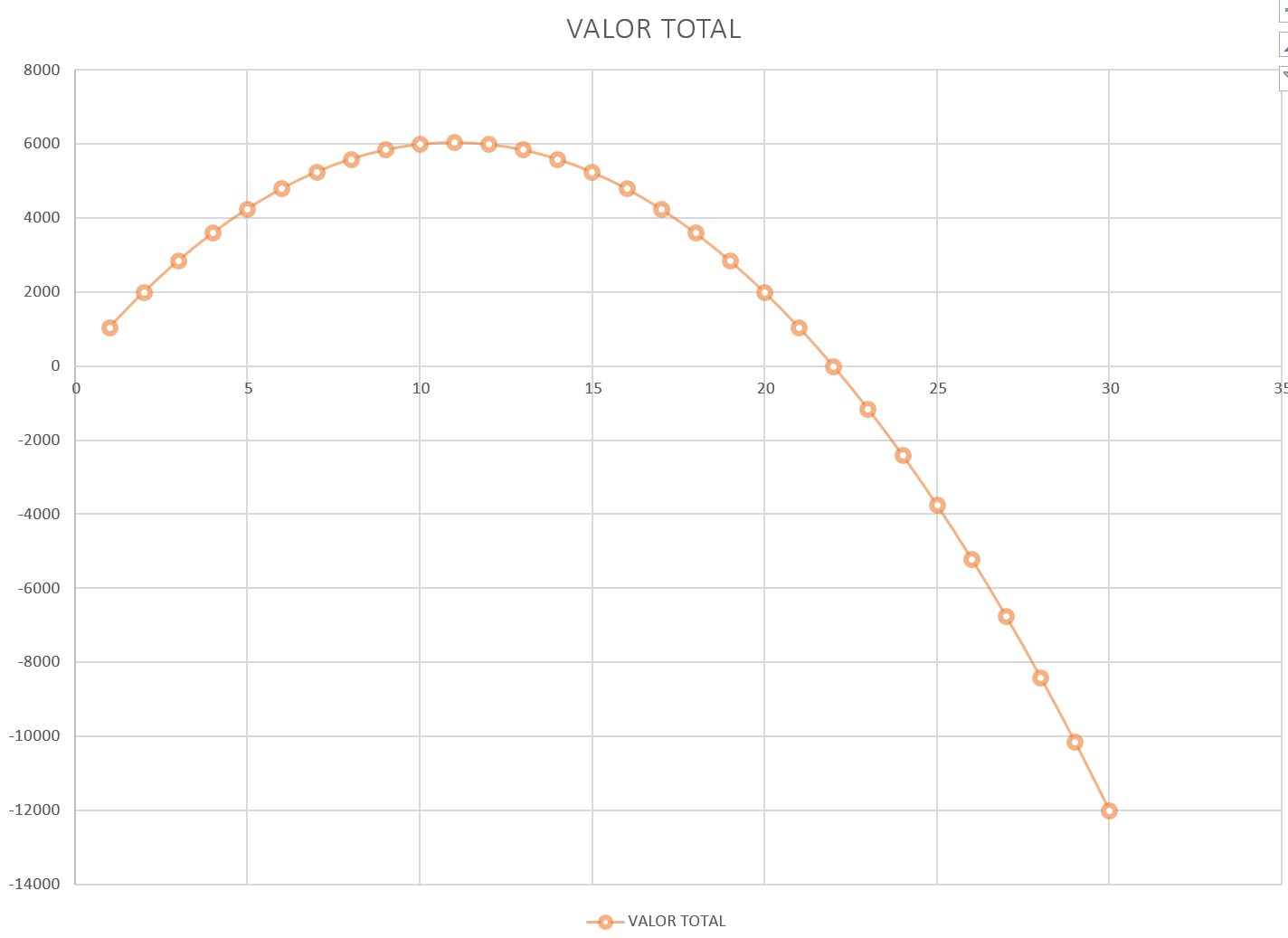
Si metemos la formula anterior a una planilla electrónica y graficamos para cada valor de k tendremos la siguiente figura
El comportamiento de este gráfico es el esperado. De la fórmula sabemos que es una parábola invertida. Su forma se debe a lo siguiente:
- Hacia la izquierda (valores de k=1, 2, ...) vemos que es siempre conveniente ir extrayendo más bloques. Esto se debe a que el incremento de un bloque de mineral (1050) es superior al costo del lastre. Sin embargo, este costo es cada vez mayor y por eso los incrementos son cada vez menores.
- Cuando k=11 alcanzamos el valor máximo posible de valor económico. Esta es la profundidad que define nuestro pit final.
- A partir de k=12, 13, ... el costo del lastre supera 1050 así que si bien seguimos ganando dinero (el valor total es positivo) es menor que en el caso k=11.
- Eventualmente, a partir de k=23 el costo es tan alto que perderíamos dinero de extraer tanto.
Solución por cónicas
Si no tenemos una planilla de cálculo a mano, o si queremos saber la solución para otros posibles valores cualesquiera (es decir no 1050 y 50 si no que P y Q), entonces podemos recurrir a nuestros conocimientos de cónicas y recordar la fórmula del vértice de una parábola. Cuando la parábola tiene ecuación
$$\Large{y = ax^2 + bx + c}$$
Recordemos que las coordenadas del vértice son (h,g) con
$$\Large{h = -\frac{b}{2a}, g= c - \frac{b^2}{4a}}$$
En nuestro caso tenemos que a=-50, b=1100 y c=50, así que las coordenadas del vértice son h=1100/100 = 11, g=6100. Estas coordenadas corresponden al valor de k y de V(k), respectivamente, es decir el valor donde se alcanza el máximo es k=11 y el valor total es 6100.
- El precio del cobre sube y ahora el beneficio de los bloques con mineral es 1500 (en vez de 1050). ¿Cuál es la profundidad óptima?
- Supongamos ahora que el valor de los bloques beneficiosos es P y que el costo por cada bloque de lastre es Q. ¿Cuál es la profundidad óptima?
- ¿Cómo se comporta el valor de k en función del valor de los bloques beneficiosos? ¿En función de los costos?
Cómputo del punto máximo utilizando derivadas
Se puede computar el punto de valor máximo de nuestra función de costos utilizando derivadas. La ecuación que describe el valor total es
$$\Large{V(k) = -50k^2 + 1100k}$$
Por lo tanto la derivada de V en función de su variable k es
$$\Large{\frac{dV}{dk}(k) = -100k + 1100}$$
Esta expresión nos da la pendiente de la función de valor total para cada punto de k. En su punto cúlmine, esta pendiente vale cero, es decir, podemos obtener el valor óptimo de k haciendo
$$\Large{-100k + 1100 = 0 \Leftrightarrow k = \frac{1100}{100} = 11}$$
Cálculo de la profundidad óptima por beneficios incrementales
Una manera alternativa de razonar para computar el valor óptimo de k es el considerar lo siguiente:
- Al extraer el primer bloque (nivel 1) ganamos 1050.
- Al extraer el segundo bloque (nivel 2), ganamos 1050, pero perdemos 2*100. El incremento es 950.
- Al extraer el tercer bloque (nivel 3), ganamos un 1050 adicional, pero perdemos 6*50. El incremento es 750.
En general vemos que al agregar un nuevo nivel, ganamos siempre 1050, pero agregamos 2*(k-1) bloques de lastre, es decir, debemos gastar -2*(k-1)*50. El valor incremental neto que percibimos por el nivel k es entonces
$$\Large{ V_{inc}(k) = 1050 - 50 \times 2 \times (k-1) }$$
Esto significa que no queremos ir agregando niveles para siempre, ya que eventualmente el incremento se hará negativo a medida que k es más grande. En el caso extremo. Queremos agregar niveles solo cuando
$$\Large{ V_{inc}(k) \geqslant 0 \Leftrightarrow 1050 - 50 \times 2 \times (k-1) \geqslant 0 \Leftrightarrow k \leqslant \frac{1050}{100} +1 = 11,5 }$$
Dado que k debe ser entero, esto significa que el mayor valor se alcanza cuando k=11.