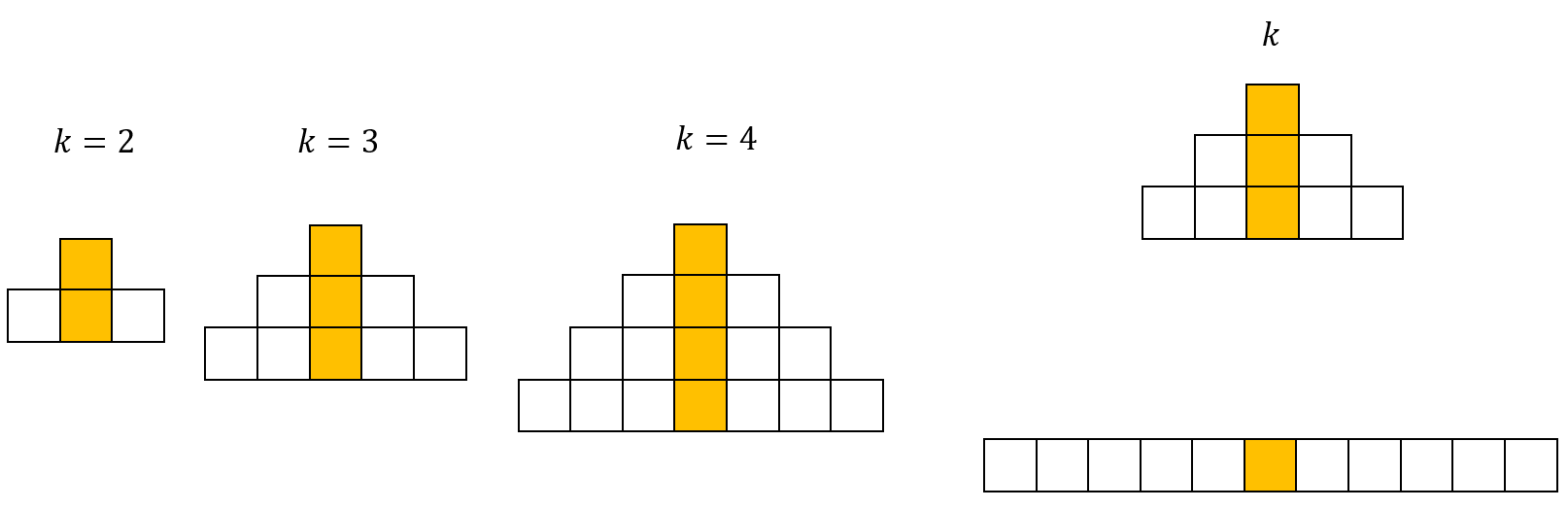Las sumatorias son una herramienta que permite hacer la adición de una secuencia de números. Se utiliza la letra griega sigma mayúscula (Σ) para representarlas.
Existen diferentes maneras de representar una sumatoria. Una bastante común corresponde a indicar el intervalo de índices de los términos que se van a sumar, lo cual corresponde a lo siguiente:
$$ \Large{\sum_{i=m}^{n} a_i = a_m + a_{m+1} + a_{m+2} + \cdots + a_{n-1} + a_{n}} $$
La i representa el índice de la sumatoria, ai representa el índice de la variable de cada término sucesivo en la serie.
Al indicar que i = m bajo el símbolo de sumatoria se está expresando que la suma debe comenzar con el término m-ésimo de la secuencia. Similarmente, la n en la parte superior indica que el último término a sumar corresponde al con índice n dentro de la secuencia.
Por supuesto, para poder realizar la adición, se debe conocer la secuencia que se está sumando. Veamos algunos ejemplos.
Ejemplo 1
Consideremos la secuencia definida por ai = i2. De esta forma a1=1, a7=49, a100=10000, etc. Tenemos entonces, por ejemplo, que
$$ \Large{\sum_{i=3}^{6} a_i = \sum_{i=3}^{6} i^2 = 3^2 + 4^2 + 5^2 + 6^2 = 86 } $$
Para la misma secuencia, solo cambiando los límites de la sumatoria, tenemos que
$$ \Large{\sum_{i=1}^{5} a_i = \sum_{i=1}^{5} i^2 = 1^2 + 2^2 + 3^2 + 4^2 + 5^2 = 55 } $$
Ejemplo 2
Volvamos a nuestro ejemplo de un modelo de bloques ficticio (después de todo, es una página de matemáticas y minería)

Podemos calcular el valor total de los bloques de la primera fila. Estos son los elementos a11, a12, ... a13. Su valor total se puede expresar en una sumatoria como
$$ \Large{\sum_{j=1}^{13} a_{1 j}} $$
Notar que cambiamos la letra del índice. Estamos usando "j" en vez de "i". Esto no cambia en nada el resultado, podemos utilizar cualquier símbolo como índice mientras no lo estemos empleando con otros fines (en este caso, por ejemplo, sería confuso usar "a").
Dado que conocemos los términos exactos, esta suma se puede calcular así:
$$ \Large {\sum_{j=1}^{6} a_{1 j} + \sum_{j=7}^{7} a_{1 j} + \sum_{j=8}^{13} a_{1 j} = \underbrace{\sum_{j=1}^{6} (-20)}_{ -20 \times 6} + \underbrace{\sum_{j=7}^{7} 100}_{100} + \underbrace{\sum_{j=8}^{13} (-20)}_{-20 \times 6} = 140} $$
Algunos ejemplos clásicos de sumas que quizás conoces son los siguientes
La suma de los n primeros números naturales
Cuenta la leyenda que cuando Gauss era un niño pequeño, su profesor(a) les planteó a él y a sus compañeros la siguiente pregunta. ¿Cuál es la suma de los primeros 100 números naturales? Es decir, cuánto es
$$ \Large{1 + 2 + 3 + \dots + 100 = ?} $$
O dicho de otra forma (con sumatorias)
$$ \Large{\sum_{k=1}^{100} k = ? } $$
El pequeño Gauss se dio cuenta de que en vez de sumar uno a uno, podía agrupar los números como muestra el siguiente diagrama.
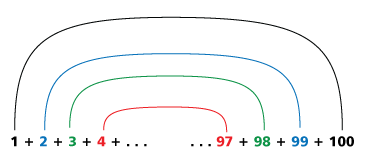
Lo cual podemos expresar como
$$ \Large{\underbrace{1+100}_{101} +\underbrace{2+99}_{101} + \underbrace{3+98}_{101} + \cdots + \underbrace{49+52}_{101} + \underbrace{50+51}_{101} }$$
Es decir
$$\Large{\sum_{k=1}^{100}k=50\times 101 = 5050}$$
Sin embargo, es posible resolver esta suma en forma general. Es decir. ¿Cuál es la suma de los primeros números n números naturales? El resultado en este caso es el siguiente
$$\Large{\sum_{k=1}^{n}k = \frac{n(n+1)}{2}}$$
La suma de los primeros números pares
En este caso el resultado es el siguiente
$$\Large{\sum_{i=0}^{n}2i = n(n+1)}$$
Notar que en este caso hemos hecho comenzar la suma desde cero, sin embargo eso no afecta de ninguna forma el resultado.
La suma de los primeros números impares
Corresponde a la siguiente fórmula
$$\Large{\sum_{i=1}^{n}2i-1 = n^2}$$
Si ya conocemos la suma de los primeros $n$ números naturales, sumar los primeros impares es simple, ya que
$$\Large{\sum_{i=1}^{n} 2i-1 = 2\sum_{i=1}^{n}i-\sum_{i=1}^{n} 1 = n(n+1)-n=n^2}$$
También podemos razonar como Gauss para resolver esta sumatoria, agrupando el último y primer término, el segundo y el penúltimo, etc. como sigue.
Si $n$ es par, vemos que la suma corresponde a
$$ \Large{1 + 3 + 5 + \cdots + (2n-5) + (2n-3) +( 2n-1) = \underbrace{1 + 2n-1}_{2n} + \underbrace{3 + 2n-3}_{2n} + \cdots + \underbrace{n/2 + 2n-n/2}_{2n}}$$
Dado que hay n/2 términos en total, el resultado es $n/2 \cdot 2n = n^2$.
Si $n$ es impar, entonces se agrupan los primeros $\frac{n-1}{2}$ términos con los $\frac{n-1}{2}$ últimos. Como antes, cada par aporta $2n$. Por otro lado el término del medio es el $i=\frac{n-1}{2}+1$ y vale $2i-1=2(\frac{n-1}{2}+1)-1=n$. El total es entonces
$$\Large{\frac{n-1}{2}\times 2n +n = n(n-1)+n=n^2}$$
Ejercicios de sumatorias
- Sabiendo el resultado para la suma de los primeros números naturales. ¿Cómo podemos usarla para deducir la fórmula para los números pares?
- Y si sabemos las otras dos, ¿cómo podemos emplearla para deducir la suma de los primeros impares?
- ¿Cuántos cuadrados hay en cada una de las siguientes pirámides?