Algunos ejemplos clásicos de sumas que quizás conoces son los siguientes

La suma de los n primeros números naturales

Cuenta la leyenda que cuando Gauss era un niño pequeño, su profesor(a) les planteó a él y a sus compañeros la siguiente pregunta. ¿Cuál es la suma de los primeros 100 números naturales? Es decir, cuánto es

$$ \Large{1 + 2 + 3 + \dots + 100 = ?} $$

O dicho de otra forma (con sumatorias)

$$ \Large{\sum_{k=1}^{100} k = ? } $$

El pequeño Gauss se dio cuenta de que en vez de sumar uno a uno, podía agrupar los números como muestra el siguiente diagrama.

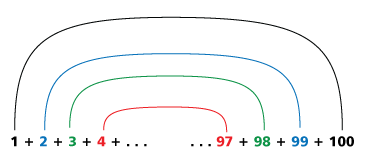
Lo cual podemos expresar como

$$ \Large{\underbrace{1+100}_{101} +\underbrace{2+99}_{101} + \underbrace{3+98}_{101} + \cdots + \underbrace{49+52}_{101} + \underbrace{50+51}_{101} }$$

Es decir

$$\Large{\sum_{k=1}^{100}k=50\times 101 = 5050}$$

 Sin embargo, es posible resolver esta suma en forma general. Es decir. ¿Cuál es la suma de los primeros números n números naturales? El resultado en este caso es el siguiente

$$\Large{\sum_{k=1}^{n}k = \frac{n(n+1)}{2}}$$

La suma de los primeros números pares

En este caso el resultado es el siguiente

$$\Large{\sum_{i=0}^{n}2i = n(n+1)}$$

Notar que en este caso hemos hecho comenzar la suma desde cero, sin embargo eso no afecta de ninguna forma el resultado.

La suma de los primeros números impares

Corresponde a la siguiente fórmula

$$\Large{\sum_{i=1}^{n}2i-1 = n^2}$$

Si ya conocemos la suma de los primeros $n$ números naturales, sumar los primeros impares es simple, ya que 

$$\Large{\sum_{i=1}^{n} 2i-1 = 2\sum_{i=1}^{n}i-\sum_{i=1}^{n} 1 = n(n+1)-n=n^2}$$

También podemos razonar como Gauss para resolver esta sumatoria, agrupando el último y primer término, el segundo y el penúltimo, etc. como sigue.

Si $n$ es par, vemos que la suma corresponde a

$$ \Large{1 + 3 + 5 + \cdots + (2n-5) + (2n-3) +( 2n-1) = \underbrace{1 + 2n-1}_{2n} + \underbrace{3 + 2n-3}_{2n} + \cdots + \underbrace{n/2 + 2n-n/2}_{2n}}$$

Dado que hay n/2 términos en total, el resultado es $n/2 \cdot 2n = n^2$.

Si $n$ es impar, entonces se agrupan los primeros $\frac{n-1}{2}$ términos con los $\frac{n-1}{2}$ últimos. Como antes, cada par aporta $2n$. Por otro lado el término del medio es el $i=\frac{n-1}{2}+1$ y vale $2i-1=2(\frac{n-1}{2}+1)-1=n$. El total es entonces

$$\Large{\frac{n-1}{2}\times 2n +n = n(n-1)+n=n^2}$$